Sprachförderung im Fachunterricht ist nicht alles, aber ohne Sprachförderung im Fachunterricht ist (fast) alles nichts. Josef Leisen
Leseförderung findet im Mathematikunterricht nicht explizit statt. Dies, obwohl für erfolgreiches Lösen vieler Mathematikaufgaben hohe Anforderungen bezüglich der Lesekompetenz gestellt werden. Diese Seite fokussiert jedoch nicht primär die Leseförderung, sondern stärker den sprachsensiblen Mathematikunterricht. Dementsprechend werden zuerst Anliegen der Sprachsensibilität im Fachunterricht besprochen, im zweiten Teil folgen Stellungnahmen zur expliziten Leseförderung. Das Dokument kann zyklusunabhängig gelesen werden. Es ist aber offensichtlich, dass Leseanfänger*innen im Kindergarten mit anderen Herausforderungen konfrontiert sind als Schulabgänger*innen. Die aufgezeigten Beispiele aus dem Unterricht sind bewusst mitten aus der Schulzeit, der 5.-Klasse, entnommen.
Sprachsensibler Mathematikunterricht

Eine erste Herausforderung stellt sich Lernenden, wenn die mathematische und die sprachliche Bedeutung einen Konflikt auslösen. Die ausgelöste Irritation, welche der abgebildeten Zahlen grösser sei, muss schliesslich in eine sinnvolle Antwort münden.
Die Frage, in welchen Unterrichtsphasen sprachliche Hürden auftauchen, könnte auch umgekehrt werden: Wann ist Sprache im Unterricht nicht relevant? Die Lehrperson erteilt einen Auftrag oder stellt eine Aufgabe. Hier ist es nicht wesentlich, ob dies in mündlicher oder schriftlicher Form erfolgt. Lernende müssen diese Aufgabenstellung entschlüsseln und da, wo es für sie nötig ist, klärende Fragen stellen. Im Anschluss wird die Problemstellung im Idealfall gelöst oder zumindest daran gearbeitet. Ergebnisse und Erkenntnisse werden zum Abschluss präsentiert. Dies wiederum kann sowohl mündlich als auch schriftlich mit den dazugehörigen Herausforderungen statt finden.
Ich-Du-Wir-Prinzip und "think-pair-share"
Erfolgreiches Mathematiklernen geschieht in unterschiedlichen methodischen Settings. Eigenständige Phasen wechseln sich mit kooperativen, dialogischen Sequenzen ab. In jeder Phase schwingen neben mathematischen Kompetenzen die sprachlichen Anforderungen mit. Gallin / Ruf sprechen seit den 90-er Jahren vom ICH-DU-WIR-Prinzip. In gleichem Sinne wird das kooperative Prinzip des «think-pair-share» verstanden.
Nachfolgende Abbildung: Ich-Du-Wir-Prinzip nach Gallin-Ruf, bzw. kooperatives Lernen nach «think-pair-share», Green-Green.
ICH mache das so!

Lernende bearbeiten in eigenständigen Phasen eine mathematische Aufgabenstellung.
Wie machst DU es?

Im Austausch besprechen Lernende andere Wege und Lösungsansätze.
Das machen WIR ab

Gemeinsam werden Konventionen getroffen und festgehalten.
Sprachsensibles Unterrichten fördern im Fach Mathematik
Warum also nicht einfach die Lernhürden senken? Vom defensiven zum offensiven Ansatz.
Defensive Strategie

Die Anforderungen (z.B. der Texte) senken, bis sie zur Kompetenz der Lernenden passen. Eine mögliche Folge: die Fossilierung der Sprachkompetenz statt deren Weiterentwicklung.
Offensive Strategie
Nur wirklich unnötige Hürden vermeiden, sonst lieber Lernende auf Hürden vorbereiten, d.h. ihre Kompetenz den Anforderungen anpassen und die Lernenden immer wieder sprachlich herausfordern.
Sprachförderung…?
Warum ausgerechnet in MEINER wertvollen Mathematik Unterrichtszeit? Kann sich um Sprachförderung nicht der Deutschunterricht kümmern?
Nein, weil...
- Für Jugendliche und Kinder mit Deutsch als Zweitsprache oder starken sprachlichen Schwierigkeiten ist eine spezifische, fachunabhängige Sprachförderung unbedingt notwendig, aber diese allein reicht nicht, denn die Lernzeit wäre allein zu gering und die sprachlichen Anforderungen des Faches sind zu speziell. Deswegen müssen alle Fächer zu allgemeinen bildungssprachlichen Kompetenzen beitragen und sich jeweils um die spezifischen fachbezogenen sprachlichen Anforderungen kümmern.
- Ein fach- und sprachintegrierter Unterricht sollte sich nur mit den sprachlichen Anforderungen beschäftigen, die fürs Fachlernen wichtig sind, nicht um künstliche, fachexterne. Dies hat sich empirisch als lernwirksam für fachliche Lernziele gezeigt und zwar sogar auch für sprachlich starke Lernende!
Sprache ist im Mathematikunterricht ein wichtiges Lernmedium, weil…
- nahezu alle (mündlich und schriftlich gestellten) Aufgaben sprachlich vermittelt sind;
- Unterrichtskommunikation auch in den gemeinsamen Arbeits- und Denkphasen in Gruppenarbeit und Klassengespräch sprachlich vermittelt ist, also z.B. alle gemeinsamen Erklärungen neuer Inhalte und Erläuterungen von Lösungswegen;
- Sprache nicht nur eine kommunikative Funktion erfüllt, sondern auch eine kognitive Funktion. Das bedeutet, sie ist nicht nur Medium zur Verständigung, sondern auch ein wichtiges Denkwerkzeug.
Dies betrifft nicht nur sprachliche Anforderungen auf Wort- und Diskursebene: Kognitiv anspruchsvolle mathematische Inhalte werden mit diskursiv anspruchsvollen Sprachhandlungen erarbeitet wie Argumentieren, Erklären mathematischer Bedeutungen und Beschreiben allgemeiner Zusammenhänge.
Worauf kommt es aus der Sicht der Lehrperson also an?
Es ist wichtig, dass Lehrpersonen…
- Sprache einfordern, d.h. möglichst reichhaltige sprachliche Äusserungen der Lernenden in den fachlichen Lernprozessen schriftlich und mündlich entlocken.
- Sprache diagnostizieren, d.h. die Lernendenäusserungen im Hinblick auf die bereits aktivierbaren Sprachhandlungen und Sprachmittel analysieren
- Sprache unterstützen, d.h. die Sprachhandlungen der Lernenden durch Bereitstellung der dafür notwendigen Sprachmittel kanalisieren
- Sprache sukzessive aufbauen, d.h. den mittelfristigen Ausbau der Sprachhandlungen und Sprachmittel und ihre zunehmend präzisere und treffsicherere Aktivierung durch gestufte Lerngelegenheiten fördern
- Fachlich relevante sprachliche Anforderungen identifizieren, d.h. die Auswahl der Sprachhandlungen und Sprachmittel für das Einfordern, Diagnostizieren, Unterstützen und sukzessive Aufbauen jeweils zu orientieren an ihrer Funktion für die fachlichen Lernziele.
Sprache und Mathematik im Lehrplan 21
Im Lehrplan 21 wird in den Bedeutungen und Zielsetzungen die Verknüpfung beider Elemente beschrieben: Mathematik als Sprache nutzen
«Mathematik ist auch eine Sprache, mit der die Ausdrucksmöglichkeiten in logischer, struktureller und visueller Hinsicht beträchtlich erweitert werden können. Ein regelmässiger Austausch zwischen Schülerinnen und Schülern trägt gleichzeitig zur Entwicklung umgangs- und fachsprachlicher Kompetenzen und zum Aufbau der Reflexionsfähigkeit bei. Der Fachbereich Mathematik regt die Erweiterung sprachlicher Kompetenzen insbesondere unter den Handlungsaspekten Mathematisieren und Darstellen und Erforschen und Argumentieren an.» In der Matrix sind, in Ergänzung zum vorgängigen Gedanken, drei Handlungsaspekte exemplarisch mit entsprechenden Sprachhandlungen verknüpft:

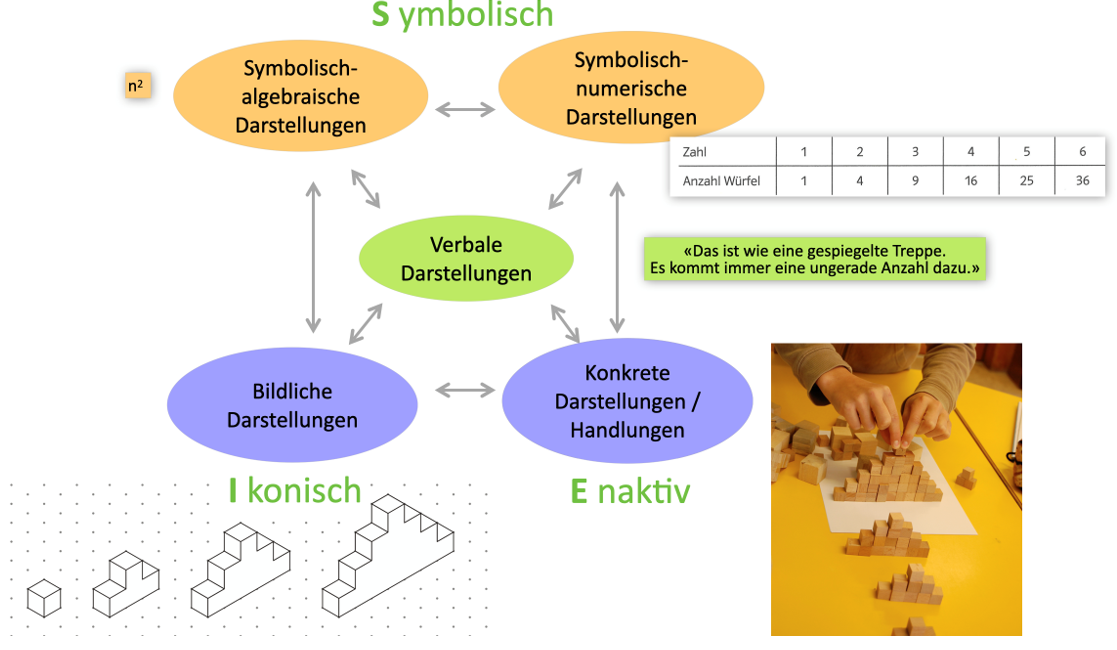
Darstellungsebenen und -Wechsel im Mathematikunterricht
J. Bruner beschrieb 1971 das EIS-Prinzip. Dieses für die Mathematikdidaktik nach wie vor gültige, an dieser Stelle zweifach erweiterte Prinzip, fokussiert verstehensorientiertes Lernen. Im Lehrplan 21 steht hierzu: «Operationen, Begriffe und Beziehungen können handelnd, bildhaft und sprachlich-symbolisch dargestellt werden. Für das verstehensorientierte Lernen ist der Wechsel zwischen diesen drei Darstellungsformen bedeutsam. Deshalb sind Lernanlässe zu schaffen, bei denen konkrete Situationen oder bildliche Darstellungen in die abstrakte Fachsprache übertragen oder umgekehrt Begriffe oder Terme konkretisiert werden.» Lernende müssen demnach in der Lage sein, zwischen den verschiedenen Darstellungsebenen zu wechseln. Hierbei kommen sprachliche Herausforderungen immer wieder zum Tragen. In diesem Sinne vernetzende Verbalisierungen dienen dem Verstehens- und Wissensaufbau in nicht zu unterschätzendem Masse.
Aufgabe der Lehrperson ist es, diesen Wechsel sprachlich korrekt und adressatengerecht zu formulieren und die Lernenden zu ermutigen, die entsprechende Fachsprache selber zu verwenden.
Hürden auf dem Weg zur Lösung des Problems
Stehen Lernende vor einem mathematischen Problem, können verschiedene Hürden identifiziert werden. Dies kann die hier im Zentrum stehende Sprache sein, ebenso der fehlende Bezug zur Sache selber oder die mangelnde Fähigkeit, das Problem mathematisch zu lösen. Als Lehrperson steht man vor der komplexen Herausforderung, möglichst umfassend und rasch zu diagnostizieren, woran das Scheitern liegt oder liegen kann:
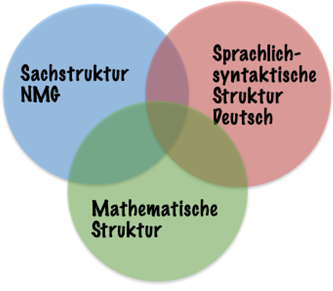
- Sachstruktur (Fach NMG)
Inhaltshürden, konzeptuelle Hürden: Es fehlen inhaltliche Vorstellungen, die zur Mathematisierung des Situationsmodells bzw. zur Interpretation der Ergebnisse gebraucht werden. - Sprachlich-syntaktische Struktur (Fach Deutsch)
Sprachhürden / Lesehürden: Lernende scheitern auf der Wort-, Satz- oder Textebene.
Strategische Hürden: Eine erfolgreiche Texterschliessung und Bildung eines Situationsmodells ist nicht möglich - Mathematische Struktur (Fach Mathematik)
Mathematikhürden: Notwendige Rechenverfahren sind auch nach erfolgreicher Mathematisierung nicht nutzbar.
Fazit
Diese kurze Auslegeordnung zeigt, mit welchen besonderen Herausforderungen sowohl Lernende wie auch Lehrpersonen im sprachsensiblen Mathematikunterricht konfrontiert sind. Hilfreich ist letzten Endes eine Sensibilisierung seitens der Lehrperson in zweifacher Hinsicht: Zum einen ist es ein sprachsensibles Nutzen der Fachsprache, um damit den Lernenden bewusst – wie auch unbewusst – eine individuelle Sprachförderung zu ermöglichen. Zum anderen gilt es, der Sprache im Verstehens- und Wissensaufbau ihre Wichtigkeit zuzugestehen und ihr damit den nötigen Platz im Unterricht einzuräumen. Man kann es «lautes Denken», «beschreiben», «begründen», «in Worte fassen», «Erkenntnisse formulieren», «bereits Verstandenes Erklären», «nach neuen Wegen suchen» nennen und vieles mehr. Sprache verknüpft Inneres mit Äusserem - und umgekehrt. Sie dient der Verbalisierung und Verfestigung von gefassten Vorstellungen und Ideen. Sie verbindet einzelne Wissenselemente miteinander und hilft, ein nachhaltiges Netz an Strategien und Konzepten aufzubauen – auch und gerade im Mathematikunterricht. Um das bewusste Planen und Einfordern geeigneter Sprachanlässe kommt die Schulmathematik nicht (mehr) herum – zumindest aus aktueller fachdidaktischer Sicht nicht, und zum Glück aller Mathematiklerneden nicht, sowohl der sprachschwächeren wie auch der wortgewandten. Damit schliesst sich der Kreis und das Eingangszitat von Leisen gewinnt mehrfach an Bedeutung.
Literatur
Prediger Susanne et al. auf http://sprachsensibles-unterrichten.de/wp-content/uploads/2018/02/SUF-Abschlussdokumentation-Mathematik.pdf sowie https://www.dzlm.de/files/uploads/WS-L07-Prediger.pdf (Abruf jeweils 01.12.2021)